Object Graphs
Object-oriented applications contain complex webs of interrelated objects. Objects are linked to each other by one object either owning or containing another object or holding a reference to another object to which it sends messages. This web of objects is called an object graph.
Even with very few objects, an application’s object graph becomes very entangled with circular references and multiple links to individual objects. Figure 1 shows an incomplete object graph for a simple Cocoa application in OS X. (Many more connections exist than are shown in this figure.) Consider the window’s view hierarchy portion of the object graph. This hierarchy is described by each view containing a list of all of its immediate subviews. However, views also have links to each other to describe the responder chain and the keyboard focus loop. Views also link to other objects in the application for target-action messages, contextual menus, and much more.
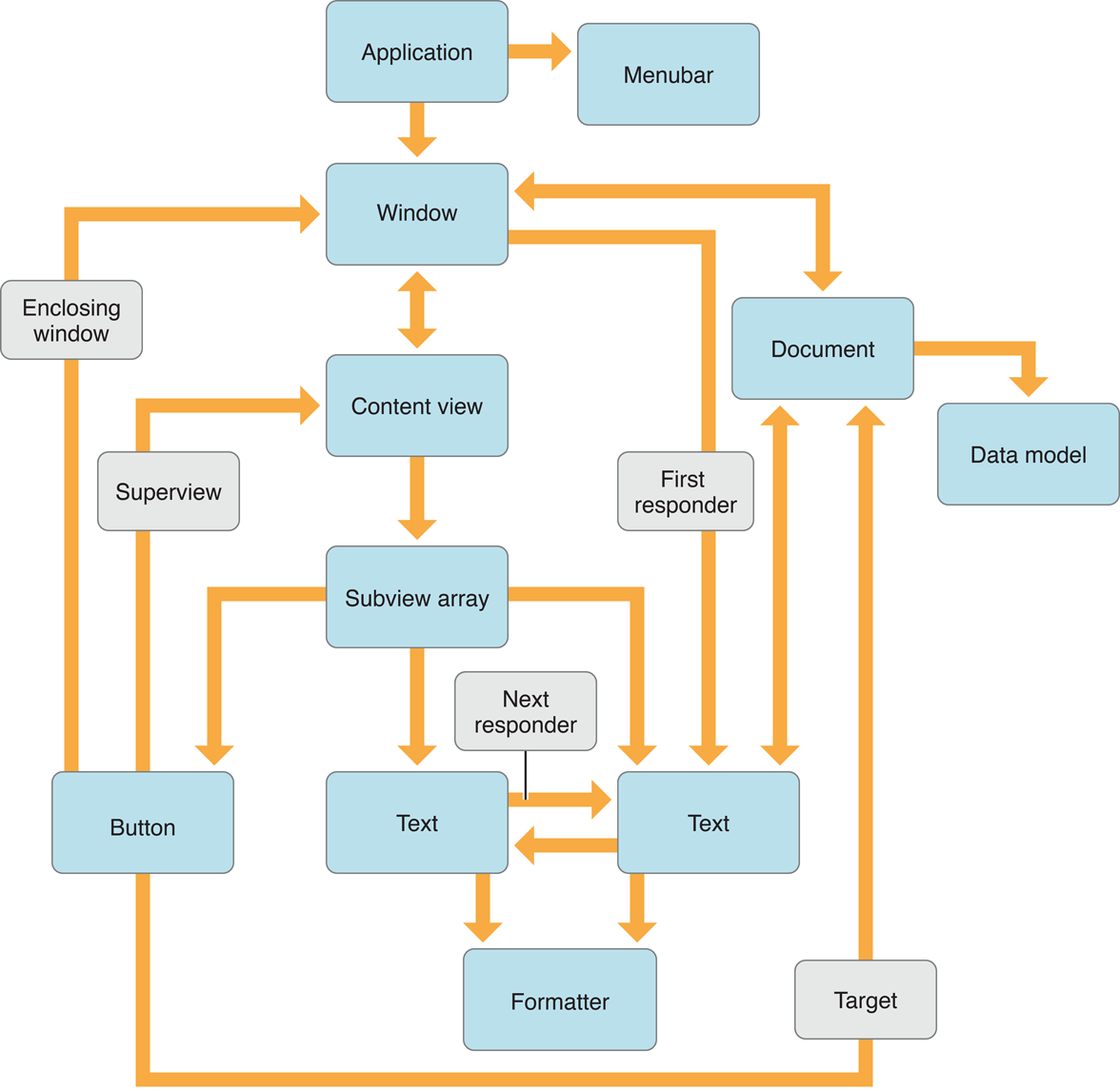
There are situations where you may want to convert an object graph, usually just a section of the full object graph in the application, into a form that can be saved to a file or transmitted to another process or machine and then reconstructed. Nib files and property lists are two examples in OS X where object graphs are saved to a file. Nib files are archives that represent the complex relationships within a user interface, such as a window’s view hierarchy. Property lists are serializations that store the simple hierarchical relationship of basic value objects. More details on archives and serializations, and how you can use them, are described in the following sections.
Archives
An archive can store an arbitrarily complex object graph. The archive preserves the identity of every object in the graph and all the relationships it has with all the other objects in the graph. When unarchived, the rebuilt object graph should, with few exceptions, be an exact copy of the original object graph.
Your application can use an archive as the storage medium of your data model. Instead of designing (and maintaining) a special file format for your data, you can leverage Cocoa’s archiving infrastructure and store the objects directly into an archive.
To support archiving, an object must adopt the NSCoding protocol, which consists of two methods. One method encodes the object’s important instance variables into the archive and the other decodes and restores the instance variables from the archive.
All of the Foundation value objects objects (NSString, NSArray, NSNumber, and so on) and most of the Application Kit and UIKit user interface objects adopt NSCoding and can be put into an archive. Each class’s reference document identifies whether they adopt NSCoding.
Serializations
Serializations store a simple hierarchy of value objects, such as dictionaries, arrays, strings, and binary data. The serialization only preserves the values of the objects and their position in the hierarchy. Multiple references to the same value object might result in multiple objects when deserialized. The mutability of the objects is not maintained.
Property lists are examples of serializations. Application attributes (the Info.plist file) and user preferences are stored as property lists.
Copyright © 2002, 2012 Apple Inc. All Rights Reserved. Terms of Use | Privacy Policy | Updated: 2012-07-17