Translating Floating Point Operations

Both AltiVec and SSE do single precision floating point arithmetic. SSE2 also does double precision floating point arithmetic. Finally, for each packed vector floating point operation on SSE or SSE2, there is also a scalar version that can be done by the vector unit that operates on only one element in the vector:

The scalar-on-vector feature is used by MacOS X on Intel to do most scalar floating point arithmetic. So, if you write a normal floating point expression, such as float a = 2.0f; that will be done on XMM. (For compiler illuminati, the GCC compiler flag, -mfpmath=sse, is on by default.) Single and double precision scalar floating point arithmetic is done on the SSE unit both for speed and also so as to deliver computational results much more like those obtained from PowerPC. The legacy x87 scalar floating point unit is still used for long double, because of its enhanced precision.

Please note that the results of floating point calculations will likely not be exactly the same between PowerPC and Intel, because the PowerPC scalar and vector FPU cores are designed around a fused multiply add operation. The Intel chips have separate multiplier and adder, meaning that those operations must be done separately. This means that for some steps in a calculation, the Intel CPU may incur an extra rounding step, which may introduce 1/2 ulp errors at the multiplication stage in the calculation. Please note that in cases involving catastrophic cancellation, this may give results that are vastly different after the addition or subtraction has completed.

SSE Floating Point Environment

The floating point environments on SSE and AltiVec are very similar. Both vector floating point units are heavily influenced by IEEE-754. Both units store their data in IEEE-754 floating point format, though, in memory, the Intel architecture stores the bytes in little endian order. Both deliver nearly the same feature set of correctly rounded basic operations, such as addition, subtraction and multiplication. (Intel is slightly richer.) For more complicated functions such as the vector versions of the standard libm transcendental operations (sin(), cos(), pow(), etc.), look to Accelerate.framework. (#include <Accelerate/Accelerate.h>). Accelerate.framework actually provides this class of operations in two different flavors:

• For simple long array computation, look to vForce.h, new for MacOS X.4.

• For vector transcendentals involving 128-bit SIMD vectors, look to vfp.h (available on all MacOS X versions).

When it comes to other aspects of IEEE-754 compliance, SSE is a bit of a step up. While AltiVec delivers the Java subset of IEEE-754, the Intel vector unit is a fully IEEE-754 compliant machine, delivering full rounding modes, exceptions and flags.

A feature comparison chart follows:

All hardware supported operations (that aren't estimates) are correctly rounded to 24 bits (float) or 53 bits (double) of precision. (The other 9/12 bits are used for exponent and sign information, exactly like PowerPC.) The accuracy of the estimates is very close to that of AltiVec, approximately 12 bits for reciprocal estimate and reciprocal square root estimate.

Denormal Handling

Neither AltiVec or SSE currently provide fast hardware support for denormals. In each case, a vector status and control register is available, with some bits that can be changed to turn on and off denormal handling. If denormal handling is turned on on a PowerPC machine and a denormal is encountered, the calculation is handled in a fast kernel trap. On a SSE enabled Intel chip the denormal is handled in hardware. As shown below, the denormal is expensive to handle in both cases:

In the table above, OFF means denormals are not handled; they are flushed to zero. ON means denormals are handled, with a 1100-1550 cycle penalty.

If one turns off denormal handling, then the two machines flush the denormals to zero and proceed as if the data they are operating on is zero. This path operates at the same cost as arithmetic on normalized numbers, at the expense of incorrect results for denormalized inputs or outputs (which are flushed to zero).

Historical use of denormals has been varied. Under MacOS 9, operating system handling of denormals was on by default, meaning that ever time you hit a denormal on MacOS 9, the machine would take a large stall while the correct result was calculated for the vector unit by the operating system. MacOS X for PowerPC ships with denormals off for AltiVec by default. (We did explore turning them on briefly in the safety and comfort of our own test labs in order to deliver more correct results for MacOS X.3, but found we were breaking some 3rd party audio code with real time data delivery needs.) However, denormal handling is on by default for PowerPC scalar floating point, where denormals are handled in hardware at no additional cost.

Under MacOS X for Intel, denormal handling is back ON by default. This is required for standards compliant operation of normal scalar floating point code, which, if you will recall, is being done by the vector unit. Since the SSE vector status and control register (MXCSR) does not differentiate between scalar and vector operations done on the vector engine, this means that the denormal handling is on by default for packed vector arithmetic too.

If you are writing code with real time delivery needs, especially audio code, you may consider turning denormals off. Please be aware that if you do so, your code, both scalar and vector (except long double) will flush denormals to zero, meaning that strictly speaking, the results will be incorrect for the set of denormalized numbers. For certain classes of computations, particularly audio, this is generally not a problem — listeners are likely unable to hear the difference between the range of denormalized numbers (0 < x < 2^126) and zero. For others, it is a problem. Proceed wisely. We recommend leaving denormal handling enabled unless you actually have a problem. Generally speaking, denormals do not happen often enough to cause trouble. However, certain classes of algorithms (most notably IIR filters) may produce nothing but denormals in certain situations (input gain goes to zero). If that occurs in a real time thread, system responsiveness may be adversely affected. Results may not be delivered on time.

To turn denormals off on AltiVec, set the Non-Java bit in the AltiVec VSCR. To turn denormals off on SSE, turn on the Denormals Are Zero and Flush to Zero (DAZ and FZ) bits in the MXCSR:

#include <xmmintrin.h>

int oldMXCSR = _mm_getcsr(); //read the old MXCSR setting

int newMXCSR = oldMXCSR | 0x8040; // set DAZ and FZ bits

_mm_setcsr( newMXCSR ); //write the new MXCSR setting to the MXCSR

... // do your work with denormals off here

//restore old MXCSR settings to turn denormals back on if they were on

_mm_setcsr( oldMXCSR );

You may also use the C99 Standard fenv.h, with the Mac OS X for Intel specific default denormals-off floating point environment.

#include <fenv.h>

#pragma STDC FENV_ACCESS ON

fenv_t oldEnv;

//Read the old environment and set the new environment using default flags and denormals off

fegetenv( &oldEnv );

fesetenv( FE_DFL_DISABLE_SSE_DENORMS_ENV );

... //do work here

//Restore old floating point environment

fesetenv( &oldEnv );

Setting and checking other bits in the MXCSR will allow you to take an exception if you hit a denormal (DM) and check to see whether you have previously hit a denormal (DE) in the vector unit, in addition to the typical IEEE-754 exceptions and flags.

Denormals also cause large stalls on the x87 scalar floating point unit. Simply loading and storing denormals in and out of the x87 unit may cause a stall. The processor has to convert them to 80-bit extended format and back during these operations. There is no way to disable denormal handling on x87.

Algorithms and Conversions

Here is a table of standard conversions for floating point operations in AltiVec and SSE:

Don't forget to convert all of those vec_madd( a, b, -0.0f) calls to _mm_mul_ps(a, b). It will save an instruction.

The most notable missing conversion in the table above is explicit floating point rounding to integer. In many cases, this can be solved by setting the appropriate rounding mode in the MXCSR and converting the vFloat to a vSInt32. This process is covered more in depth in the conversions section below. However, that only works if the floating point value is representable as a 32-bit integer. Since many do not fit into the 32-bit signed integer range, it may be necessary to use a full precision floor function. The basic operation involves adding a large magic number to the vFloat, then subtracting it away again. The number is chosen such that the unit in the last place of the magic number corresponds to the 1's binary digit. This value is 2^23, 0x1.0p23f. This causes rounding at that position according to the processor's rounding mode after the addition. When 2^23 is subtracted away again, the value will be restored, but correctly rounded to integer value.

There are some tricks to this process. Negative numbers may require that you reverse the order of the add and subtract, or use 2^24. With some clever programming you may be able to avoid toggling the MXCSR to set rounding modes and come up with an algorithm that works for all four rounding modes. Depending on your specific application, you may be able to avoid some or all of these steps. In the simplest case, it is just an add and a subtract. Here is some sample code for floor and trunc.

static inline vFloat _mm_floor_ps( vFloat v ) __attribute__ ((always_inline));

static inline vFloat _mm_floor_ps( vFloat v )

{

    static const vFloat twoTo23 = (vFloat){ 0x1.0p23f, 0x1.0p23f, 0x1.0p23f, 0x1.0p23f };

    vFloat b = (vFloat) _mm_srli_epi32( _mm_slli_epi32( (vUInt32) v, 1 ), 1 ); //fabs(v)

    vFloat d = _mm_sub_ps( _mm_add_ps( _mm_add_ps( _mm_sub_ps( v, twoTo23 ), twoTo23 ), twoTo23 ), twoTo23 ); //the meat of floor

    vFloat largeMaskE = (vFloat) _mm_cmpgt_ps( b, twoTo23 ); //-1 if v >= 2**23

    vFloat g = (vFloat) _mm_cmplt_ps( v, d ); //check for possible off by one error

    vFloat h = _mm_cvtepi32_ps( (vUInt32) g ); //convert positive check result to -1.0, negative to 0.0

    vFloat t = _mm_add_ps( d, h ); //add in the error if there is one

    //Select between output result and input value based on v >= 2**23

    v = _mm_and_ps( v, largeMaskE );

    t = _mm_andnot_ps( largeMaskE, t );

    return _mm_or_ps( t, v );

}

static inline vFloat _mm_trunc_ps( vFloat v ) __attribute__ ((always_inline));

static inline vFloat _mm_trunc_ps( vFloat v )

{

    static const vFloat twoTo23 = (vFloat){ 0x1.0p23f, 0x1.0p23f, 0x1.0p23f, 0x1.0p23f };

    vFloat b = (vFloat) _mm_srli_epi32( _mm_slli_epi32( (vUInt32) v, 1 ), 1 ); //fabs(v)

    vFloat d = _mm_sub_ps( _mm_add_ps( b, twoTo23 ), twoTo23 ); //the meat of floor

    vFloat largeMaskE = (vFloat) _mm_cmpgt_ps( b, twoTo23 ); //-1 if v >= 2**23

    vFloat g = (vFloat) _mm_cmplt_ps( b, d ); //check for possible off by one error

    vFloat h = _mm_cvtepi32_ps( (vUInt32) g ); //convert positive check result to -1.0, negative to 0.0

    vFloat t = _mm_add_ps( d, h ); //add in the error if there is one

    //put the sign bit back

    vFloat sign = (vFloat) _mm_slli_epi31( _mm_srli128( (vUInt32) v, 31), 31 );

    t = _mm_or_ps( t, sign );

    //Select between output result and input value based on fabs(v) >= 2**23

    v = _mm_and_ps( v, largeMaskE );

    t = _mm_andnot_ps( largeMaskE, t );

    return _mm_or_ps( t, v );

}

Translating Integer Operations

Most integer operations on SSE are in the SSE2 segment of the vector extensions. Packed vector integer arithmetic first debuted on the Intel platform in MMX. The same operations were later redeployed on the XMM register file in SSE2. All vector integer instructions generally start with the letter P (for packed). Most integer instructions come in two flavors with the same name, one for MMX and one for XMM. For a complete list, please see the Intel Architecture Software Developer's Manual, Volumes 2. (Link available at the top of this page.) Because the two share the same name and use of MMX can damage x87 floating point state, it may be advisable in certain circumstances to employ GCC compiler flags such as -mno-mmx, to avoid inadvertently using MMX.

Integer Add / Subtract / Min / Max

You will find the full complement of modulo adds and subtracts on SSE2. In addition, SSE2 also does 64-bit modulo addition and subtraction. The AltiVec vec_addc and vec_subc for large-precision unsigned integer addition and subtraction do not have SSE counterparts, however. It is suggested that you use the 64-bit adder to handle your extended integer precision.

SSE2 supports saturated addition for 8- and 16-bit element sizes only. Min and Max functions are available for vUInt8 and vSInt16, only.

Integer Multiplication

One of the more difficult problems to solve when translating AltiVec to SSE is what to do about integer multiplication. There is almost no overlap between AltiVec and SSE for integer multiplication. The AltiVec vec_mladd operation is a little bit like _mm_mullo_epi16, and vec_msum is a little bit like _mm_madd_epi16, but they are by no means a close match. There are 5 integer multipliers on SSE2:

One shared calculation motif that works reasonably well between AltiVec and SSE is the concept of full precision multiplies, where two vectors with element of size N, multiply to create two product vectors with element size 2N. On AltiVec, this is done with vec_mule and vec_mulo, followed by vec_merge to interleave even and odd results. On SSE, you can use the low and high 16 bit multiplies, with a merge operation (see _mm_unpacklo_epi16 and _mm_unpackhi_epi16).

The other shared calculation motif that works well is to exploit commonalities between _mm_madd_epi16 and vec_msum( vSInt16, vSInt16, vSInt32 ). Finally, in a very small number of cases, you can use _mm_mullo_epi16(a,b) interchangeably with vec_mladd(a,b,0).

Integer Algorithms and Conversions

Here is a table of simple AltiVec to SSE translations for integer arithmetic:

Note 1: Something similar can be done with _mm_mulhi_epi16 and vec_add(s)_epi16. However, _mm_mulhi_epi16 shifts right by 16, and the AltiVec instruction shifts right by 15, so some change in fixed point format will be required.

//AltiVec: multiply a * b and return double wide result in high and low result

void vec_mul_full( vSInt32 *highResult, vSInt32 *lowResult, vSInt16 a, vSInt16 b)

{

    vSInt32 even = vec_mule( a, b );

    vSInt32 odd = vec_mulo( a, b );

    *highResult = vec_mergeh( even, odd );

    *lowResult = vec_mergel( even, odd );

}

//SSE2: multiply a * b and return double wide result in high and low result

void _mm_mul_full( vSInt32 *highResult, vSInt32 *lowResult, vSInt16 a, vSInt16 b)

{

    vSInt32 hi = _mm_mulhi_epi16( a, b );

    vSInt32 low = _mm_mullo_epi16( a, b );

    *highResult = _mm_unpacklo_epi16( hi, low );

    *lowResult = _mm_unpackhi_epi16( hi, low );

}

Translating Compare Operations

Testing Inequalities

Vector compares are done on SSE in substantially the same way as for AltiVec. The same basic set of compare instructions (similar to vec_cmp*) are available. They return a vector containing like sized elements with -1 for a true result and 0 for a false result in the corresponding element. The floating point compares provide the full set that AltiVec provides (except vec_cmpb) and in addition provide ordered and unordered compares and the != test. In addition, all vector floating point compares come in both scalar and packed versions.

The integer compares test for equality and inequality. The inequality test are for signed integers only. There are no unsigned compare greater than instruction. There are no compare instructions for 64-bit types.

Conditional Execution

Branching based on the result of a compare is handled differently from AltiVec, however. The AltiVec compares set some bits in the condition register, upon which the processor can branch directly. SSE compares set no analogous bits. Instead, use MOVMSKPD, MOVMSKPS or PMOVMSKB instruction to copy the top bit out of each element, crunch them together into a 2- ,4- or 16-bit int for double, float and integer data respectively, and copy to an integer register. You may then test that bit field to decide whether or not to branch. This example implements the SSE version of AltiVec's vec_any_eq intrinsic for vFloat:

int _mm_any_eq( vFloat a, vFloat b )

{

    //test a==b for each float in a & b

    vFloat mask = _mm_cmpeq_ps( a, b );

    //copy top bit of each result to maskbits

    int maskBits = _mm_movemask_ps( mask );

    return maskBits != 0;

}

If you are branching based on the result of a compare of one element only, then you can do the whole thing in one instruction using either UCOMISD/UCOMISS or COMISD/COMISS.

Select

Branching is expensive on Intel, just as it is on PowerPC. Most of the time that a test is done, the developer on either platform will elect not to do conditional execution, but instead evaluate both sides of the branch and select the correct result based on the value of the test. In AltiVec, this would look like this:

// if (a > 0 ) a += a;

vUInt32 mask = vec_cmpgt( a, zero );

vFloat twoA = vec_add( a, a);

a = vec_sel( a, twoA, mask );

In SSE, the same algorithm is used. However, SSE has no select instruction. One must use AND, ANDNOT,, OR instead:

vFloat _mm_sel_ps( vFloat a, vFloat b, vFloat mask )

{

    b = _mm_and_ps( b, mask );

    a = _mm_andnot_ps( mask, a );

    return _mm_or_ps( a, b );

}

Then, the SSE version of the above AltiVec code may be written:

// if (a > 0 ) a += a

vFloat mask = _mm_cmpgt_ps( a, zero );

vFloat twoA = _mm_add_ps( a, a);

a = _mm_sel_ps( a, twoA, mask );

We have found that in practice, it is sometimes possible to cleverly replace select with simpler Boolean operators like a single AND, OR or XOR, especially in vector floating point code. While not a performance win for AltiVec (it's a wash), for SSE this replaces three instructions with one, and can be a large win for code that uses select frequently. Very infrequently, sleepy AltiVec programmers may momentarily forget about vec_min and vec_max, and use compare / select instead. Those are a nice win too, when you can find them.

Algorithms and Conversions

Here is a conversion table for AltiVec to SSE translation for vector compares and select:

Translating Conversion Operations

SSE has a wide variety of data type conversions. Like AltiVec, if you wish to simply use a vector of one type (e.g. vFloat) as a vector of another type (e.g. vSInt32) without changing the bits, you can do that with a simple typecast:

vFloat one = (vFloat) {1.0f, 1.0f, 1.0f, 1.0f };

vSInt32 oneBits = (vSInt32) one;

The variable oneBits will now contain {0x3f800000, 0x3f800000, 0x3f800000, 0x3f800000}, the bit pattern for a vector full of 1.0f. This is a free operation, requiring at most one instruction to copy the data between registers, but in the optimum case no work needs to be done. (Note: please see caution about moving data between vector int, float and double types, under “MMX” in theInstruction Overview section.)

However, if you wish to convert one type of vector to another with retention of numerical value (instead of bit pattern) then you will wish to use the appropriate conversion instruction. Conversions among different types generally follow the same pathway as for AltiVec, except that 16 bit pixels are not really a native data type for SSE. There is no hardware conversion between 16-bit pixel and vUInt8. The rest of the conversions are described below:

Float - Int Conversions

Conversions between floating point and integer types are similar to AltiVec with a few differences:

• The vec_ctf, vec_ctu and vec_cts instructions take a second parameter, an immediate to be used to adjust the power of two of the result. The SSE conversion functions take no second parameter. To do this power of 2 scaling on SSE, multiply the floating point input or output by the appropriate power of 2.

• In the float-to-int direction, floating point input values larger than the largest representable int result in 0x80000000 (a very negative number) rather than the largest representable int on PowerPC.

• There are no unsigned conversions between int and float

• All four rounding modes are available directly through the MXCSR. You won't need vec_floor, vec_trunc, vec_ceil, vec_round to round before you do the conversion to int. There are two different flavors of float-to-int conversion: _mm_cvtps_epi32 and _mm_cvttps_epi32. The first rounds according to the MXCSR rounding bits. The second one always uses round towards zero.

• Conversions between vDouble and vSInt32 are also available.

Here is how to fix the overflow saturation difference for vFloat to vSInt32 conversions:

const vFloat two31 = (const vFloat) {0x1.0p31f,0x1.0p31f,0x1.0p31f,0x1.0p31f};

//Convert float to signed int, with AltiVec style overflow

//(i.e. large float -> 0x7fffffff instead of 0x80000000)

vSInt32 _mm_cts( vFloat v )

{

    vFloat overflow = _mm_cmpge_ps( v, two31);

    vSInt32 result = _mm_cvtps_epi32( v );

    return _mm_xor_ps( result, overflow );

}

Here is a function that does vFloat to vUInt32 conversion, that gives the correct results, with AltiVec saturation for out of range inputs. You can write faster functions if you are willing to sacrifice correctness or saturate differently:

static inline vUInt32 _mm_ctu_ps( vFloat f )

{

    vFloat two32 = _mm_add_ps( two31, two31);

    vFloat zero = _mm_xor_ps(f,f);

    //check for overflow before conversion to int

    vFloat overflow = _mm_cmpge_ps( f, two31 );

    vFloat overflow2 = _mm_cmpge_ps( f, two32 );

    vFloat subval = _mm_and_ps( overflow, two31 );

    vUInt32 addval = _mm_slli_epi32((vUInt32)overflow, 31);

    vUInt32 result;

    //bias the value to signed space if it is >= 2**31

    f = _mm_sub_ps( f, subval );

    //clip at zero

    f = _mm_max_ps( f, zero );

    //convert to int with saturation

    result = _mm_cvtps_epi32( f ); //rounding mode should be round to nearest

    //unbias

    result = _mm_add_epi32( result, addval );

    //patch up the overflow case

    result = _mm_or_si128( result, (vUInt32)overflow2 );

    return result;

}

Some special case short-cuts for float-to-unsigned int conversion:

• If you do not need the complete unsigned range, you may consider just using the float to signed conversion, with some possible preclipping using _mm_min_ps and _mm_max_ps.

• If you do not mind throwing away the least significant (up to) 8 bits of your result for values in the range -2^24 < f < 2^24, this can be done more quickly by subtracting 0x1.0p31f from your floating point input, doing the signed conversion, then subtracting 0x80000000 from the result.

Finally, the vUInt32 to vFloat conversion can be done using the signed conversion, 16-bits at a time:

const vFloat two16 = (const vFloat) {0x1.0p16f,0x1.0p16f,0x1.0p16f,0x1.0p16f};

//Convert vUInt32 to vFloat according to the current rounding mode

static inline vFloat _mm_ctf_epu32( vUInt32 v )

{

    // Avoid double rounding by doing two exact conversions

    //of high and low 16-bit segments

    vSInt32 hi = _mm_srli_epi32( (vSInt32) v, 16 );

    vSInt32 lo = _mm_srli_epi32( _mm_slli_epi32( (vSInt32) v, 16 ), 16 );

    vFloat fHi = _mm_mul_ps( _mm_cvtepi32_ps( hi ), two16);

    vFloat fLo = _mm_cvtepi32_ps( lo );

    // do single rounding according to current rounding mode

    // note that AltiVec always uses round to nearest. We use current

    // rounding mode here, which is round to nearest by default.

    return _mm_add_ps( fHi, fLo );

}

Once again, if you don’t care about the last few bits of precision and correctly rounded results or the high half of the unsigned int range, then you can probably speed things up a bit.

Int - Int Conversions

Int - Int conversions change the size of vector elements. This in turn changes the number of vectors required to hold the data to either twice as many or half as many, depending on whether the elements are getting larger or smaller. The basic method by which data conversions are done is the same between AltiVec and SSE. A few details differ.

Int - Int Conversions (Large to Small)

Conversion of larger int types into smaller int types will mean converting two vectors to one. Formally, these come in saturating and non-saturating variants, to take care of the case where the value of the integer input exceeds the value representable in the smaller result integer. AltiVec provides both styes. SSE provides only the saturating variety. To do unsaturated pack on SSE, use a left and right shift to truncate the data into the appropriate range. (For signed data, use a right algebraic shift. For unsigned data, use a right logical shift.) This will prevent the saturated pack instructions from doing any saturation. Example, pack two vUInt16's down into a vUInt8 without saturation:

vUInt8 vec_pack_epu16( vUInt16 hi, vUInt16 lo );

We would like to use _mm_packus_epi16 for this. Unfortunately, values outside the range [0,255] will pack with saturation yielding 0 or 255 as the result. What is more, since the instruction takes signed input, and we have unsigned inputs, values larger than 32768 will get truncated to 0 instead of 255. To fix that, we whack off the high bits. This can be done by AND-ing with (vUInt16)(0x00FF). :

vUInt8 vec_pack_epu16( vUInt16 hi, vUInt16 lo )

{

    const vUInt16 mask = (const vUInt16){0x00ff, 0x00ff, 0x00ff, 0x00ff, 0x00ff, 0x00ff, 0x00ff, 0x00ff };

    // mask off high byte

    hi = _mm_and_si128( hi, mask );

    lo = _mm_and_si128( lo, mask );

    return _mm_packus_epi16( hi, lo );

}

If you need to return a signed unsaturated result, then use a right algebraic shift instead, and the appropriate signed saturated pack. In this case, we have to use the shift. The AND won't do the appropriate sign extension:

vSInt8 vec_pack_epu16( vUInt16 hi, vUInt16 lo )

{

    // shift hi and lo left by 8 to chop off high byte

    hi = _mm_slli_epi16( hi, 8 );

    lo = _mm_slli_epi16( lo, 8 );

    // shift hi and lo back right again (algebraic)

    hi = _mm_srai_epi16( hi, 8 );

    lo = _mm_srai_epi16( lo, 8 );

    return _mm_packs_epi16( hi, lo );

}

A number of saturated packing instructions are missing, such as vSInt32 to vUInt16. In such cases, it may be required that you add / subtract small biases from the value so that the pack operation works correctly, then subtract / add them back out after the pack is complete. In some circumstances, this may be further complicated by the lack of a 32-bit saturated add.

Int - Int Conversions (Small to Large)

Conversion of smaller int types to larger int types will mean converting one vector into two. SSE handles this in the same way AltiVec does, using high and low flavors of the conversion to handle the high and low halves of the vector. While AltiVec provides both signed and unsigned unpack primitives (the unsigned ones are vec_merge(0,v)), SSE provides only the unsigned variety.

To convert unsigned ints to larger unsigned ints, simply unpack with zero:

//SSE translation of vec_mergeh( 0, v )

vUInt32 vec_unpackhi_epu16( vUInt16 v )

{

    vUInt16 zero = _mm_xor_si128( v, v );

    return (vUInt32) _mm_unpackhi_epi16( v, zero );

}

Observe that the argument order for the unpack instruction is backwards from AltiVec. As discussed later, this may become further confused by byte swapping.

To convert signed ints into larger signed ints, simply merge with itself, then right algebraic shift to do the sign extension:

//SSE translation of vec_unpackh( 0, v )

vSInt32 vec_unpackhi_epi16( vSInt16 v )

{

    //depending on your view of the world, you may want

    //_mm_unpacklo_epi16 here instead

    vSInt32 t = (vSInt32) _mm_unpackhi_epi16( v,v );

    return _mm_srai_epi32( t, 16 );

}

Algorithms and Conversions

Here is a conversion table for AltiVec to SSE translation for data type conversions:

Note 1: Sample code appears under “Float - Int Conversions”

It is likely that a number of the vec_packs and vec_packsu translations above reported as "none" do exist. However, we haven't found any that simultaneously work for all possible inputs and which also perform satisfactorily. Where possible, the first choice is to find some other format to pack the data into that is supported well by the Intel vector ISA. In other cases, you may be aware that certain classes of inputs do not happen in your particular function. This may reduce the problem space a bit and allow for a much more efficient solution.

Translating Permute Operations

As we shall describe in the vec_perm and shuffle section to follow, the Intel permute capability isn't as flexible as AltiVec. Generally speaking, it is not possible to permute data in a data dependent way — that is, except for self-modifying code, the order of the reshuffling must be known at compile time. This means that the Intel permute unit (as defined by the series of instructions in MMX, SSE, SSE2, and SSE3) cannot be used for lookup tables, to select pivot elements in register, to do misalignment handling, etc., unless the exact nature of the permute is known at compile time.

Things are not quite so bleak as they may appear at first. It is frequently true that there is a workaround for this sort of untranslatable functionality. Left or right 128-bit octet shifts which used to be handled by lvsl and vperm might instead be handled with some clever misaligned loads. MMX has arbitrary left and right shifts on its 64-bit registers. Lookup tables can still be done the old fashioned way, with separate loads for each element. (This is a bit easier under Intel, because scalar loads go to a defined place in the vector. Loading and splatting a scalar on AltiVec is perhaps unnecessarily unwieldy.) Finally, certain transformations (e.g. byte swapping) can be accomplished in a few vector instructions, in place of one permute.

Caution: Would be users of the Intel permute unit should be aware that the x86 memory architecture is little endian. Data is byte-swapped on load and store in and out of the vector unit. The swap occurs over the entire 16-byte vector, like this:

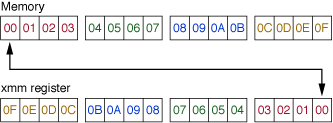
As described more fully in the loads and stores segment below, this means that both the ordering of bytes within each elements and the order of elements within the vector are reversed. This can make permutes confusing. If your left shifts go right, and your right shifts go left, and all your attempts at permute do the wrong thing, you may have forgotten that you are working on a little endian machine.

Merge

AltiVec's vec_mergeh and vec_mergel intrinsics translate directly to _mm_unpackhi and _mm_unpacklo. Vector unpacks are available for 8-, 16-, 32- and 64-bit data varieties.

Which flavor (high or low) to use and what order to place the arguments in is complicated by the little endian storage format. Under AltiVec, vec_mergeh(even,odd) could be used for a wide variety of purposes. On a big endian system, these are all degenerate. On a little endian system, they fall into a couple of classes for interleaving and unpacking data, which to further complicate things can be viewed based on the order of data as it appears in register, or following a store to memory:

• Interleaving data — let's say you start with left and right audio channels, each in its own vector, and you need to make an interleaved audio stream consisting of data in the order {left, right, left, right, ...}. On AltiVec, you'd just use vec_merge(left, right) and be done with it. On SSE you must first take into account the fact that this is a little endian system and memory order is the important one! This means that you actually want { ..., right2, left2, right1, left1, right0, left0} in register, so that you get {left0, right0, left1, right1, left2, right3, ...} when you store it out. That means you will be using _mm_unpacklo to replace vec_mergeh. In addition, the first argument of _mm_unpacklo is the one that goes in the odd position, whereas for vec_mergeh, the first argument would go into the even position. This means that vec_mergeh( even, odd) translates to _mm_unpacklo(even,odd) for data viewed in memory order, and _mm_unpackhi( odd, even ) to replace vec_mergeh if the data is viewed in register order.

• Enlarging data — if you are using vec_mergeh to convert ints to larger ints (e.g. the SSE equivalent of converting a vector unsigned short to a pair of vector unsigned ints), then everything changes. In this case, one wants a different set of swaps to occur on storage to memory, so as to preserve the high / low order of the two elements. To be brief, vec_mergeh( high, low ) maps to _mm_unpacklo( low, high ) for data viewed in memory order, and _mm_unpackhi( low, high ) for data viewed in register order.

Shifts and Rotations

SSE provides a series of shift operations for most vector types, including 64-bit shifts and 128-bit octet shifts. The exception is 8-bit vector types, for which no shifts are available. For the rest, you may shift left or right. Right shifts come in the familiar logical (zero fill) and algebraic (sign extend) formats. Algebraic shifts are only available for 16- and 32-bit element sizes. A feature table follows:

For all supported types except 128-bit shifts, you may shift either by an immediate value, known at compile time, or by a value present in a XMM vector. 128-bit shifts are by immediate only. The shift by value capability is different from AltiVec, however, in that while AltiVec allows you to shift each element in the vector a different amount from its fellows, on SSE all elements must be shifted by the same amount, the quantity held in the right-most element (register element order).

SSE has no rotate instructions. If you need to rotate a M-bit element by N-bits, you'll need to shift left by N bits, shift another copy right by M-N bits and OR the results together.

vec_perm and shuffle

In certain cases, it is possible to translate vec_perm to SHUFPS, SHUFPD, PSHUFHW, PSHUFLW or PSHUFD. The permute map must be known at compile time, and the data movement pattern must be supported by one of the above instructions. There are no shuffles capable of data organization at the byte level (apart from _mm_unpack). They all operate on 16-, 32- or 64-bit elements.

Many uses of vec_perm are not supported by SSE. It is frequently necessary to abandon permute based algorithms, when moving to SSE. In some cases, it may even be necessary to abandon SSE altogether and fall back on scalar code. However, in most cases this is not necessary. Most of the tough permute cases are linked to misalignment handling or scatter loading. Typically the best approach for these sorts of problems is to use the misaligned vector loads or scalar loads in SSE to do the work, rather than rely on the permute unit. Since scalar loads place data in a defined place in the register, it is typically easier on SSE to do scatter loading.

Loads and Stores

A point should probably be made at the outset of this discussion, because it is one that is underemphasized in discussions about SIMD vector units in general. The Load / Store Units (LSUs) underlying most SIMD architectures (including both AltiVec and SSE) are not in themselves SIMD units. That is, you can't load or store to multiple addresses in parallel in a single instruction (unless they are contiguous, and therefore representable by a single address). Each LSU operates on only one address at a time. Your only opportunity to increase apparent parallelism is to make your single load or store do more work by loading or storing more bytes at a time. Apart from that, there is no SIMD-style parallelism in the LSU.

Why is this relevant? It is important to understand that while the vector unit is highly efficient for arithmetic, there should be no expectation of enhanced speed from the LSU portion of the AltiVec or SSE vector hardware compared to scalar code, except where loads or stores of large (up to 128-bit) chunks do the work of multiple smaller scalar loads or stores. Since every bit of data that you do arithmetic on must be first loaded into register, the LSU is potentially a bottleneck. If you want enhanced parallelism from the LSU, the only way to do that is to arrange your data in a contiguous format so that you can load in as much data as possible in as large a chunk as possible using a single address, do the calculation, then store the result out in a single big contiguous chunk. If your data is scattered throughout memory, this is not possible. Your vector code will spend a lot of time doing lots of little loads trying to coalesce scattered data into vectors and then even more time trying to scatter the results back out to memory using lots of little stores. If that isn't enough, there are also profound cache inefficiencies to accessing your data that way. Poor data layouts can nullify the vector advantage and even make vector code run slower than scalar code in some cases.

Vector data should be kept together, preferably in aligned, uniform arrays so that it can be accessed in as big a chunk as possible. This is doubly important on SSE, where misaligned loads and stores cannot reach the same peak theoretical throughput as aligned loads and stores, and where the permute unit is much less capable at reordering data. If you are vectorizing a body of code for the first time, you should give serious thought to how your data is organized into memory. If you already have AltiVec code, then translating to SSE should be a snap, because you probably already did that work when writing the AltiVec code.

Misalignment

SSE provides aligned and misaligned loads and stores in three different flavors: integer, single precision floating point and double precision floating point. It is suggested that you use the appropriate load and store for the data that you are working on. The aligned and misaligned loads and stores are simple and easy to use and shouldn't require too much explanation, except for the caution that the aligned variants will trigger an illegal instruction exception if they are passed a misaligned address.

There are no Least Recently Used variants on the loads and stores. (Note: the G5 ignores the LRU amendment and treats lvxl and stvxl as lvx and stvx.) There are however non-temporal stores. These cause the store to be written directly to memory. If the address maps to entries in the cache, the cache data is flushed out with the store. These can provide large performance increases, but should be used with caution. You only want to use them with data that you aren't going to need again for a while. Non-temporal stores require use of a SFENCE synchronization primitive before the data may be loaded back in again to ensure a coherent memory state.

The method of handling misaligned 128-bit vector loads and stores is nearly orthogonal between AltiVec and SSE. While you can do aligned loads on SSE like AltiVec, SSE lacks the concatenate-and-shift-by-variable capability that AltiVec has (done with lvsl, vperm). Though SSE has 128-bit shifts (by octet), they take immediates which must be known at compile time, preventing their use for misalignment. In most cases, it is required to use the misaligned load and store instructions when one needs to access data of unknown alignment. This means that your AltiVec misalignment handling code is probably not directly translatable to SSE. You'll likely need to rewrite that segment of the function with entirely new code to handle misalignment the SSE way.

Misaligned stores are much slower than misaligned loads. They should be avoided whenever possible. Typically the right thing to do with misaligned arrays is have a small scalar loop that iterates until it reaches a store address that is aligned, then skip to vector code to do as many aligned stores as possible, then do a bit more scalar calculation at the end. With some clever code design, it is also possible to use misaligned stores at either end of the array and aligned stores for the middle. This can be a little complicated if the function operates in place.

Keep in mind that the different misalignment handling strategies carry along with them different rules about when it is safe to do what. For example, it is always safe to load an aligned vector as long as at least one byte in the vector is valid data. However, it is only safe to load a misaligned vector if all the bytes in the misaligned vector are valid data. Thus, while you may have frequently read a few bytes past the end of misaligned arrays with AltiVec (which only supports aligned vector loads — misalignment is handled in software), you may not do that safely using SSE, where misaligned loads are directly supported in hardware and using aligned loads to access misaligned data is generally not done because the requisite shift instruction is missing.

The Intel hardware prefetchers are generally much more agile and able than similar hardware on PowerPC. If you do need to prefetch, you may use the GCC extension __builtin_prefetch( ptr ). This works on PowerPC, as well. It fetches a cacheline containing the address pointed to by ptr.

Scalar Loads and Stores

SSE provides a rich set of scalar loads and stores. MOVQ and MOVD can be used to move 8- and 4-byte integers to and from the low element on the XMM vector. These instructions can also be used to move the same amount of data to and from the MMX and r32 registers, which is a feature unknown to PowerPC. So, while there are no 16-bit and 8-bit element loads and stores, one can do a byte or 16-bit word load or store using the scalar integer registers, and use MOVD to move data between the integer registers and the vector unit.

Similarly, there are scalar floating point move instructions for single and double precision floating point, MOVSS and MOVSD. These likewise place or use the data in the low element of the XMM register. They can be used to move data between XMM registers as well.

Be aware that when the destination operand is an XMM register, the move element instructions will zero the rest of the destination register. Element loads and stores do not have alignment restrictions. Because alignment is handled so differently between AltiVec vector element loads and stores and SSE vector element loads and stores, segments of code that rely on these operations will in many cases need to be rewritten.

SSE element loads and stores are very important to the SSE architecture. More so than for AltiVec, element loads and stores are frequently the solution to difficult permute problems.

x86 is Little Endian!

As mentioned before (see Figure 4-1), elements of a vector and the bytes within the elements are reversed when stored in register. If your data looks like this in code:

float f[4]= { 0.0f, 1.0f, 2.0f, 3.0f };

vFloat v = _mm_loadu_ps( f );

The data in v will look like this:

v = { 3.0f, 2.0f, 1.0f, 0.0f }

Don't worry! If you store the data back out, it will be swapped again and appear in the original order shown by f[4]. The order is only backwards in register. (The bytes inside the elements themselves are in big endian byte order in register. The swap on store, makes the bytes in the elements little endian and restores the order of the elements to the expected order.)

If your permutes all seem to be broken, and left shifts go right and right shifts go left, it is likely you've forgotten about this element ordering reversal.

Performance Tips

• Shark it! Shark is still the best way to identify performance problems. This will help you determine what to vectorize. The system trace facility will show you what other problems need to fixed to make vectorization the win it should be. There is no cycle accurate simulator available for Intel at this time.

• Unroll Different. You may have unrolled N-way in parallel on PowerPC. The Intel architecture is much narrower, and tolerates serial data dependencies better. Indeed, serial data dependencies get better throughput for some stages of the pipeline (register allocation) than does simple access of named registers. Generally speaking, the compiler can handle this form of unrolling for you, saving you time. There are no aliasing problems to worry about.

• Register spillage is expensive. Don't believe everything you read about really fast loads and stores. They are fast, but they still take time. If you are spilling data out on the stack, those loads and stores usually are taking significant time that could have been used for something else.

• Reduce or eliminate your need for the permute unit. It is not as strong as on AltiVec. You could find yourself spending all your CPU time solving permute problems rather than doing actual work. (This was already a problem for AltiVec!) Reorganize your data in memory so that it doesn't need to be reorganized in the permute unit. Align data whenever possible. Many permute problems can be solved a different way by loading in data differently, taking advantage of Intel's many different MOV instructions.

• Don't bother synthesizing constants on the fly like you did for AltiVec. Most of the time, you won't have register space to keep those constants in register. You also don't have vec_splat_*, so synthesizing constants takes a lot longer.

• See if you can replace vec_sel with simpler Boolean operations like AND, ANDNOT, XOR or OR. You can save two instructions and maybe a register or two every time you manage to do that.

• It is still just as worthwhile to pay attention to cache usage. You can prefetch data using the GCC extension, __builtin_prefetch(). If you need to store out data and won't need to use it again for a while, the non-temporal stores might be a large win. These flush the cash, so be careful. They aren't always a win!

• If you store out multiple small pieces of data (e.g. four floats in float[4]) and then load in a large piece of data (e.g. a vFloat) that covers that same area, this causes a large stall, because the floating point stores need to flush out all the way to the caches before the data is available. Store forwarding doesn't work in that case. While unions are a handy way to do data transfer, they can get you into trouble too.

• Just like AltiVec, denormal stalls can be very expensive. Unlike AltiVec, you are much more likely to encounter them.

• While translating code from AltiVec to SSE, pay attention to the expense of each translation. Some AltiVec instructions translate directly to a single SSE equivalent, while another potentially very similar instruction may take a dozen SSE instructions to do. Sometimes, it is better to be flexible about which one you use, rather than translate verbatim — convert floats to signed ints, rather than unsigned, if you don't need the extra range. Other times, you might want to rewrite the core logic of an algorithm to emphasize the strengths of both vector architectures, not just one.

• AltiVec is a rich ISA. This gives you a lot of freedom. There are frequently three ways to do anything, one of which is highly unintuitive but delivers a miracle in two instructions. SSE is smaller. Usually, the obvious way to do something is the best way. Keep it simple.

• SSE involves destructive instructions most of the time. If you can phrase your algorithm in terms of destructive logic, you can probably save some unnecessary copies, and possibly some register spillage. (This will probably preclude software pipelining. However, software pipelining may not be necessary because the Intel processors are highly out-of-order.)

• Heed cautions and tips in the Intel Processor Optimization Reference Manual.