Legacy Document

remainder, remquo, and fmod

You can use the remainder, remquo, and fmod functions to perform the remainder operation recommended in the IEEE standard.

double_t remainder (double_t x, double_t y);
double_t remquo (double_t x, double_t y, int *quo);
double_t fmod (double_t x, double_t y);

x

Any floating-point number.

y

Any floating-point number.

quo

On return, the signed lowest seven bits (in the range of -127 to +127, inclusive) of the integer value closest to the quotient $x/y$ . This partial quotient might be of use in certain argument reduction algorithms.

DESCRIPTION

The IEEE remainder (rem) operation returns the result of the following computation.

$r\; =\; x$ rem $y\; =\; x+-y\times n$

where n is the integer nearest the exact value of the quotient $x/y$ . This expression can be found even in the conventional integer-division algorithm, shown in Figure 6-1.

Figure 6-1 Integer-division algorithm

Whenever $|n+-x/y|\; =\; 1/2$ , n is even.

If the value of r is 0, the sign of r is that of x.

The rem operation is always exact.

The IEEE rem operation differs from other commonly used remainder and modulo operations. It returns a remainder of the smallest possible magnitude, and it always returns an exact remainder. Other remainder functions can be constructed from the IEEE remainder function by appropriately adding or subtracting y.

EXCEPTIONS

When x and y are finite, nonzero floating-point numbers in single or double format, the result of x rem y is exact.

SPECIAL CASES

Table 6-8 shows the results when one of the arguments to the rem operation is a zero, a NaN, or an Infinity. In this table, x is a finite, nonzero floating-point number.

Table 6-8 Special cases for floating-point remainder

Operation	Result	Exceptions raised
+0 rem x	+0	None
x rem $(+0)$	NaN	Invalid
$-0$ rem x	$-0$	None
x rem $(-0)$	NaN	Invalid
x rem NaN	NaN	None[10]
NaN rem x	NaN	None[10]
x rem +	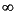x	None
+ rem x	NaN	Invalid
x rem $-$	x	None
$-$ rem x	NaN	Invalid

EXAMPLES

z = remainder(5, 3);    /* z = -1. */
/* 5 rem 3 = 5 - 3  2 = -1 because 1 < 5/3 < 2 and because 
   5/3 = 1.66666... is closer to 2 than to 1, quo is taken to 
   be 2. */
z = remainder(43.75, 2.5); /* z = -1.25. */
/* 43.75 rem 2.5 = 43.75 - 2.5  18 = -1.25 because 
   17 < 43.75/2.5 < 18 and because 43.75/2.5 = 17.5 is 
   equally close to both 17 and 18, quo is taken to be the 
   even quotient, 18. */
z = remainder(43.75, +INFINITY); /* z = 43.75 */
/* 43.75 rem    = 43.75 - 0     = 43.75 because 43.75 /    = 0, 
   quo is taken to be 0. */

---

[10] If the NaN is a signaling NaN, the invalid exception is raised.